前情提要

在做金融时序收益率预测时，尤其在需要按照分位数来选择标的回测的情况下，我们可能会希望使用 Rank IC（可理解为秩相关性）作为评价收益率预测能力的标准。然而在深度学习中，这一指标却无法直接作为损失函数使用，因为反向传播要求损失函数的计算是可微的，而 rank 计算却是不可微分的。

为了解决这一问题，Soft Rank 算法应运而生。

Soft Rank 简介

以我的理解，Soft Rank 算法是一种近似算法， 能够在允许一定误差的情况下给出一个数列的 rank 值。比如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import torch

ts = torch.randn(1, 10, requires_grad=True)
print("Original data:\n", ts)
print("Rank of data:\n", torch.tensor(rankdata(ts.detach().numpy()), dtype=torch.float32))
print("Soft ranked data:\n", soft_rank(ts, regularization_strength=0.1))

"""
Original data:
 tensor([[-0.2936,  1.3017, -0.7662,  1.9435, -1.1154, -0.4187,  1.0562,  0.8975,
         -1.7620,  1.5031]], requires_grad=True)
Rank of data:
 tensor([ 5.,  8.,  3., 10.,  2.,  4.,  7.,  6.,  1.,  9.])
Soft ranked data:
 tensor([[ 5.,  8.,  3., 10.,  2.,  4.,  7.,  6.,  1.,  9.]],
       grad_fn=<StackBackward0>)
"""

可以看到，soft_rank 函数输出的值是近似于真实 rank 的，同时它还保留了 Tensor 的梯度信息，便于进行反向传播运算。

Soft Rank 应用

接下来介绍两种我接触过的 Soft Rank 算法实践。

方法 1：Soft Rank 直接实现

以下给出直接用 PtTorch 原生方法实现 Soft Rank 的算法：

1
2
3
4
5
6
7
8
9
10
11
12
def soft_rank(y, regularization_strength=1.0):
    # 计算所有 pairwise 差异，形状为 (n, n)
    pairwise_diff = y.t() - y

    # 应用 sigmoid 函数
    sigmoid_vals = torch.sigmoid(pairwise_diff / regularization_strength)

    # 计算每个元素的 soft rank
    ranks = sigmoid_vals.sum(dim=1)

    # 标准化
    return ranks / y.shape[0]

注意这一函数最终输出的结果与真正的 Rank 分布可能有很大差异，比如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import torch

ts = torch.randn(1, 10, requires_grad=True)
print("Original data:\n", ts)
print("Rank of data:\n", torch.tensor(rankdata(ts.detach().numpy()), dtype=torch.float32))
print("Soft ranked data:\n", soft_rank(ts, regularization_strength=0.1))

"""
Original data:
 tensor([[-0.7919,  2.1005, -0.8140, -0.0836,  0.7290,  0.5838,  0.9163, -0.0866,
          1.0455,  0.7178]], requires_grad=True)
Rank of data:
 tensor([ 2., 10.,  1.,  4.,  7.,  5.,  8.,  3.,  9.,  6.])
Soft ranked data:
 tensor([1.5000, 9.5000, 0.5000, 3.4509, 6.5000, 4.5000, 7.5000, 2.5491, 8.5000,
        5.5000], grad_fn=<DivBackward0>)
"""

不过这一差异对于相关性的计算没有任何影响。

方法 2：fast-soft-sort by Google Research

凭借 Google 对 Fast Differentiable Sorting and Ranking 的研究和开发，我们有了可以直接调用的 Soft Sort 和Soft Rank 的工具：fast-soft-sort。使用方式相当简单：

1
2
3
4
5
6
7
8
9
10
from fast_soft_sort.pytorch_ops import soft_rank

ts = torch.randn(1, 10, requires_grad=True)
print("Soft ranked data:\n", soft_rank(ts, regularization_strength=0.1))

"""
Soft ranked data:
 tensor([5.5000, 3.5000, 6.5000, 1.5000, 4.5000, 7.5000, 2.5000, 8.5000, 0.5000,
        9.5000], grad_fn=<DivBackward0>)
"""

方法比较

从性能上看，方法 2 远超 方法 1。

fast-soft-sort 的时间复杂度为 $O(n\log{n})$，空间复杂度为 $O(n)$，而直接实现的函数时间复杂度和空间复杂度都是 $O(n^2)$。实践上看也的确如此，当数列长度大于 5000 时，两者性能差异就已经很明显了，这里就不进一步测试了。

当然，方法 1 也不是没有优点，它直接使用 PyTorch 内置方法实现，无需引入其他库。另外，fast-soft-sort 底层算法使用 NumPy 实现，因此必须先将 Tensor 通过 .cpu() 转移到 CPU 上进行计算，再转移回 GPU 中，这也会带来一定的性能消耗。好在，也有人实现了 Torchsort，它采用了和 fast-soft-sort 相同的算法，但是使用 PyTorch 内置方法实现。我没有使用过这一工具，感兴趣的读者可以自行尝试。

Soft Rank 参数

你可能注意到，两种方法都存在 regularization_strength 这一参数。这个参数的效果如下：

优缺点参数较大时参数较小时
优点相关系数梯度较大，可能更容易收敛rank 值估算更精确，秩相关系数误差较小
缺点rank 值估算更粗糙，秩相关系数误差较大相关系数梯度较小，可能不容易收敛

且在参数不变的情况下，样本量增大同样会导致估计精确程度的下降。但是估计精度仅仅是对于 soft rank 后数值的分布而言。无论参数如何，soft rank 后数值的顺序都是完全正确的。

不同参数下估计准确程度对比

首先，生成两组随机数据进行测试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
import torch

# 设定样本数量
num_samples = 5000

# 均值
mu = np.array([0, 0])

# 协方差矩阵
r = np.array([
    [1, 0.5],
    [0.5, 1]
])

# 调用相关函数，生成随机数
rng = np.random.default_rng()
y = rng.multivariate_normal(mu, r, size=num_samples)

y_true = torch.tensor(y[:, 0], dtype=torch.float32, requires_grad=True).reshape(-1, 1)
y_pred = torch.tensor(y[:, 1], dtype=torch.float32, requires_grad=True).reshape(-1, 1)

此时，两组数据分布如下：

两组数列分布图

以下两图展示了在不同参数下，同一组数据使用 soft_rank 计算的结果与精确计算 rank 的结果的相关性：

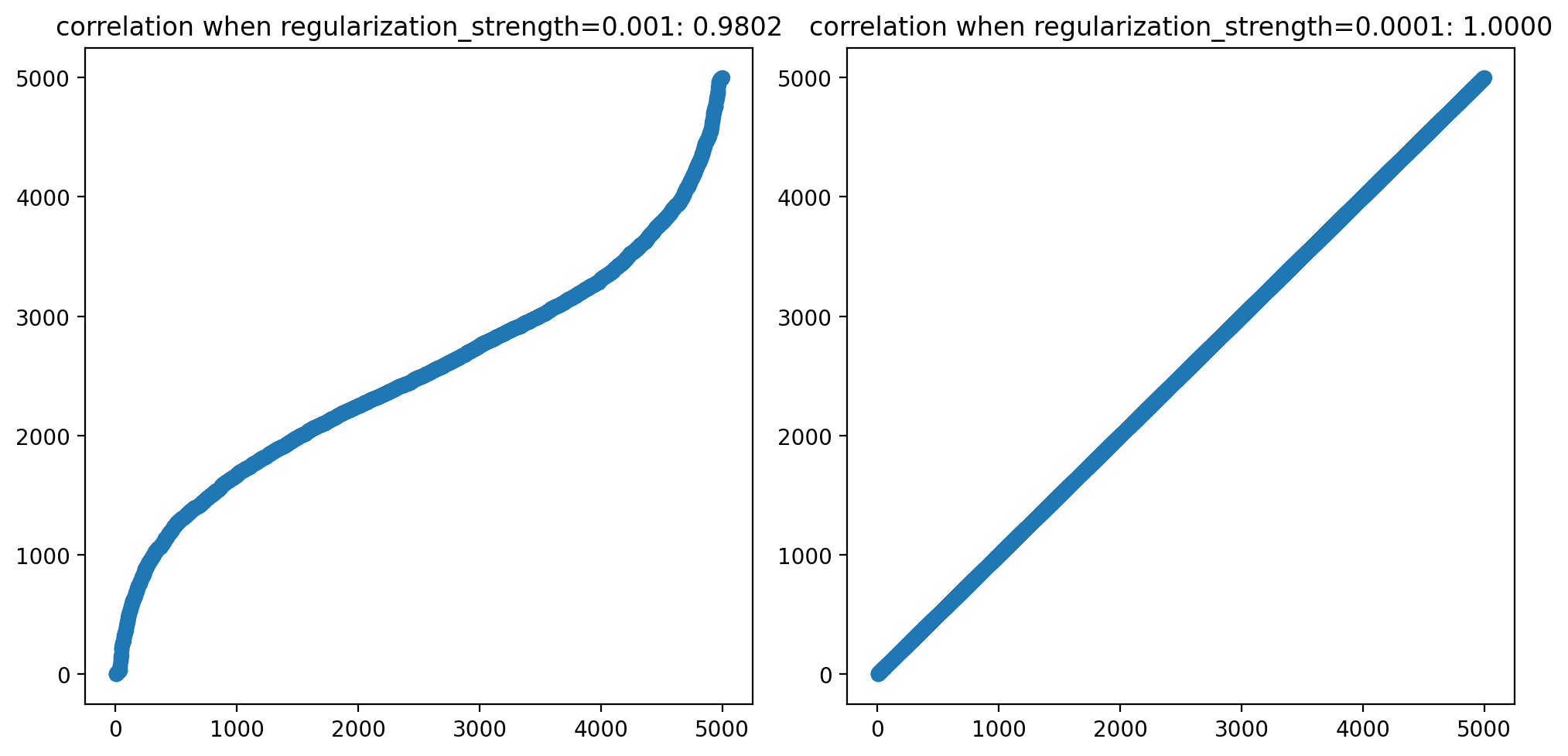
不同参数下，估算值与精确值相关性展示

此时，在我预设的数据下，计算出来的相关系数为

精确 Rank IC参数为 0.001 时 Soft Rank IC参数为 0.0001 时 Soft Rank IC
0.468441814184188840.47642540931701660.46844363212585

不同参数下 Rank IC 梯度对比

下图绘制了当 regularization_strength 分别取值为 0.001 和 0.0001 的情况下，以及直接计算 IC（而非 Rank IC）的情况下，IC 的梯度向量中数值的分布，并标注了每个分布的 25% 和 75% 分位的位置。

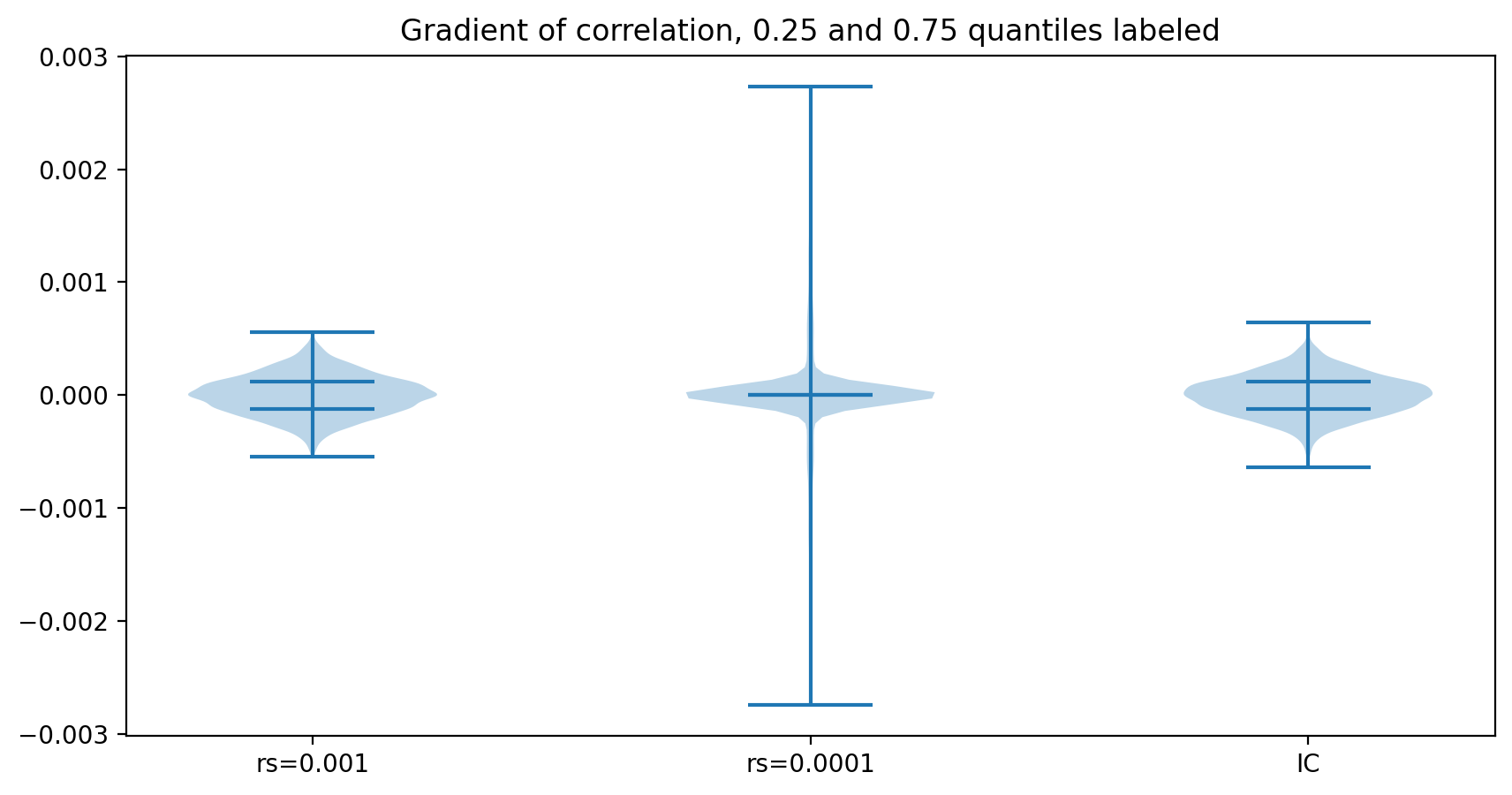
不同参数下以及 IC 计算后梯度向量数值分布

可以看到，当 regularization_strength 取值为 0.001 时，梯度向量中数值的分布与直接计算 IC 相似，但当取值为 0.0001 时，梯度向量中数值除了少数离散值以外，数量级都很小，以至于 25% 和 75% 分位线都无法分辨。

结论

  • 相比方法 1，方法 2 的复杂度远远更低，从性能角度考虑，如果没有特别需求，建议使用方法 2。
  • regularization_strength 除了影响估算精度以外，也会影响梯度的分布。实际应用时，应当充分考虑两边的利弊来调整参数。