量化实习 v2丨Day 50:不合预期但确实神奇的期限结构因子
条评论今日花了一天时间,好好检查了一下数据和程序逻辑,重点检查是否使用了未来数据;接着将目前为止所做的工作写了一份报告提交给带教,真够折腾的。
尽管做策略的时候已经很小心了,但是果然还是在不经意间引入了未来数据。而罪魁祸首就是 pandas.DataFrame.resample() 这一方法。
pandas 的 resample() 之谜
使用这一方法的场景是,由于我的回测框架无法设置调仓频率,因此不得不通过将因子值降频来保证非调仓交易日的因子值与上一交易日的因子值相同,以此来达到不调仓的效果。要做到这一点,我的思路是先将因子 resample() 一下,取最后一个值,然后再通过 reindex() 回到之前的因子格式,举例如
1 | # use resample() to resample |
然而这一方法的使用却出现了意外:resample() 的重采样是严格的,在它想要采样的时点,如果该时点不在原本的 index 中,就会将上一个找到的值强行作为这一时点的采样值。而因子值的 index 是确实了大量日期的,因为一部分日期不是交易日。这就会导致,有的重采样点会出现在非交易日,造成最后结果不符合预期。
为了保证按照原数据的 index 来重采样,就需要用到 DataFrame 的 groupby() 方法,如
1 | # use groupby() to resample |
期限结构因子
上一篇日记提到,我主要研究了两个期限结构因子:
展期收益率因子
$$
R_t = \left[\ln{\left(P_{t,n}\right) - \ln{\left(P_{t,d}\right)}} \right] \times {365\over N_{t,d} - N_{t,n}}
$$
其中,$P_{t,n}$ 和 $P_{t,d}$ 分别代表 $t$ 日近月合约与远月合约的价格,而 $N_{t,d}$ 和 $N_{t,n}$ 则分别代表远月合约和近月合约的到期日距离 $t$ 日天数。由于我手头数据并无合约到期日信息,因此我舍弃了因子结构的后半部分,实际上因子结构为
$$
R_t = \ln{\left(P_{t,n}\right) - \ln{\left(P_{t,d}\right)}}
$$
变得更简单了。
这里能够调整的参数主要有二:
- 持仓周期天数;
- 所选近月合约与远月合约组合,包括最近月合约与主力合约、最近月合约与次近月合约和最近月合约与最远月合约等。
展期收益率可以理解为将近月合约平仓并向后展期到远月合约,这两个期货合约间的价差。若因子值为正说明近月合约价格高于远月合约价格,给出做多信号;反之则给出做空信号。
基差动量因子
$$
basis\ momentum=\prod^t_{i=t-R+1}\left(1+R^{T_1}_{fut,i}\right)-\prod^t_{i=t-R+1}\left(1+R^{T_2}_{fut,i} \right)
$$
这一因子在一个给定的滚动窗口中反复计算两个合约的累计收益率,并作差来得到基差动量数值。其中,$R^{T_1}_{fut,i}$ 和 $R^{T_2}_{fut,i}$ 分别代表近月合约和远月合约在 $i$ 日的收益率,$R$ 表示计算累计收益率的窗口,得到的是 $t$ 日的因子值。
这里能调整三类参数:
- 持仓周期天数;
- 所选近月合约与远月合约组合,包括最近月合约与主力合约、最近月合约与次近月合约和最近月合约与最远月合约等;
- 滚动窗口大小 $R$。
因子值越大,说明近月合约价格的上涨幅度超过远月合约价格越多,则价差越可能回归,因此给出越强的做多信号;相反则给出越强的做空信号。
回测结果
以下回测均考虑 0.02% 的交易费率。
展期收益率因子
对最近月合约与主力合约组合、最近月合约与次近月合约组合、最近月合约与最远月合约组合分别测试因子绩效。
最近月合约与主力合约组合
因子结构简单,但是有效。这一因子最有效的合约组合是最近月合约与主力合约。在这一组合下,因子收益率对参数不敏感,基本都能获得稳定收益,只是收益率有差别,这与因子带来的信息衰减和交易费率都有关。以 10 个交易日的持仓周期为例,本地回测结果:
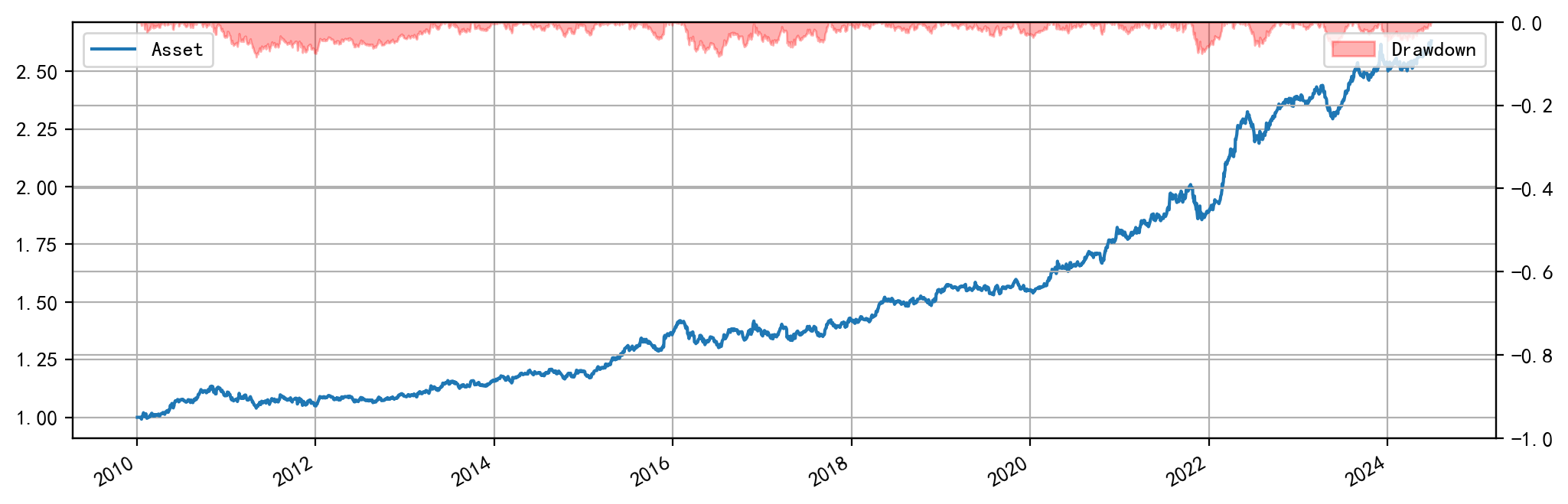
夏普比率能够达到 1.17。
其他合约组合
然而若尝试其他合约组合则会出现各种问题。无论是使用近月合约与次近月合约的组合,还是近月合约与最远月合约的组合,用同样的方式计算因子并回测的结果却呈现完全相反的结果。以最近月合约与最远月合约为例:
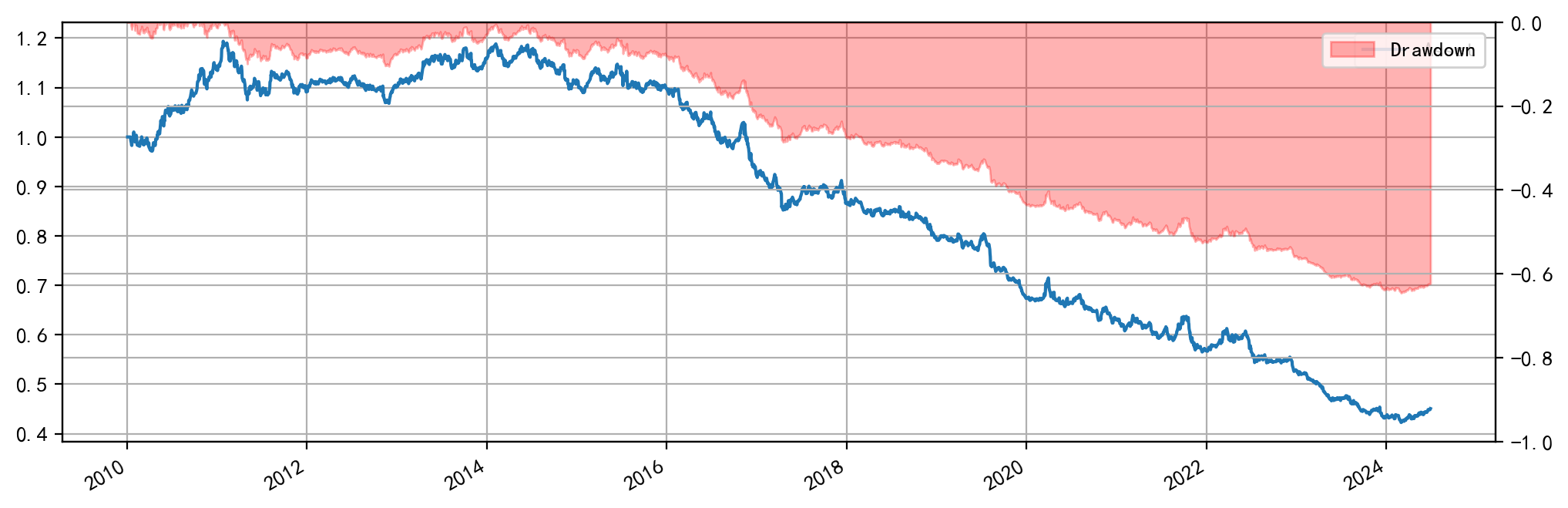
基差动量因子
由于这一因子存在更多参数,因此可以通过网格寻参来寻找较优参数。接下来,我将持有周期设为左轴,滚动窗口设为上轴来展示寻参结果,并仅展示回测的夏普比率数值。
最近月合约与主力合约组合
使用这一组合时,在本地回测能够得到较好收益曲线。本地参数网格搜索结果如下:
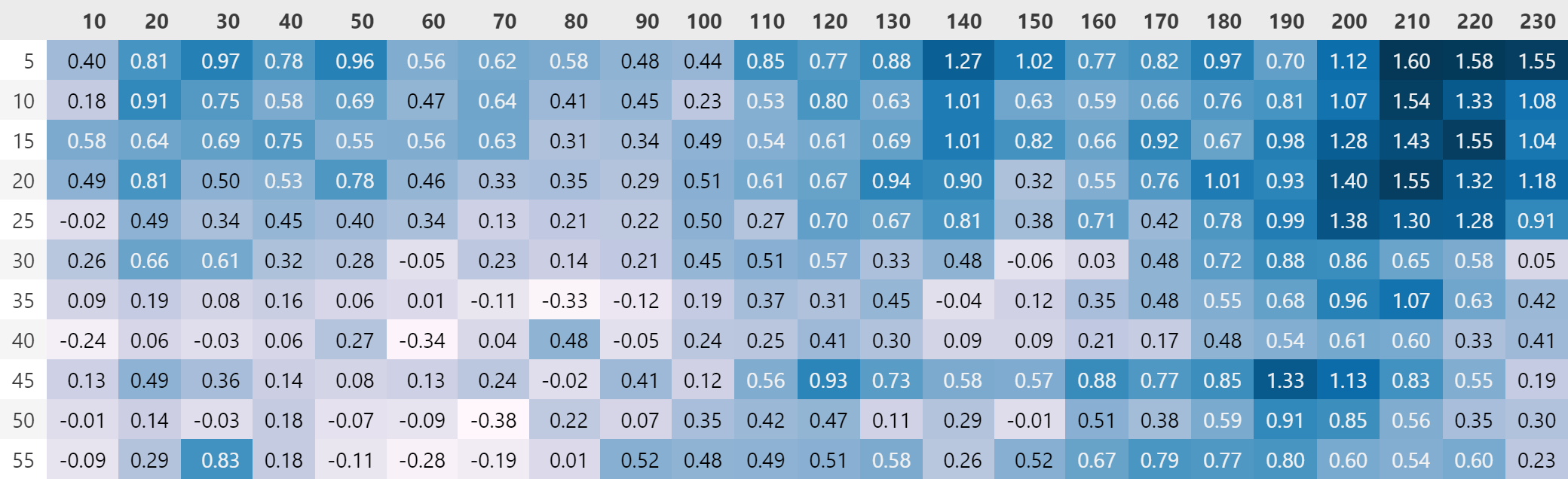
以回测结果较好的参数组合 (20, 210) 为例,回测结果如下图:
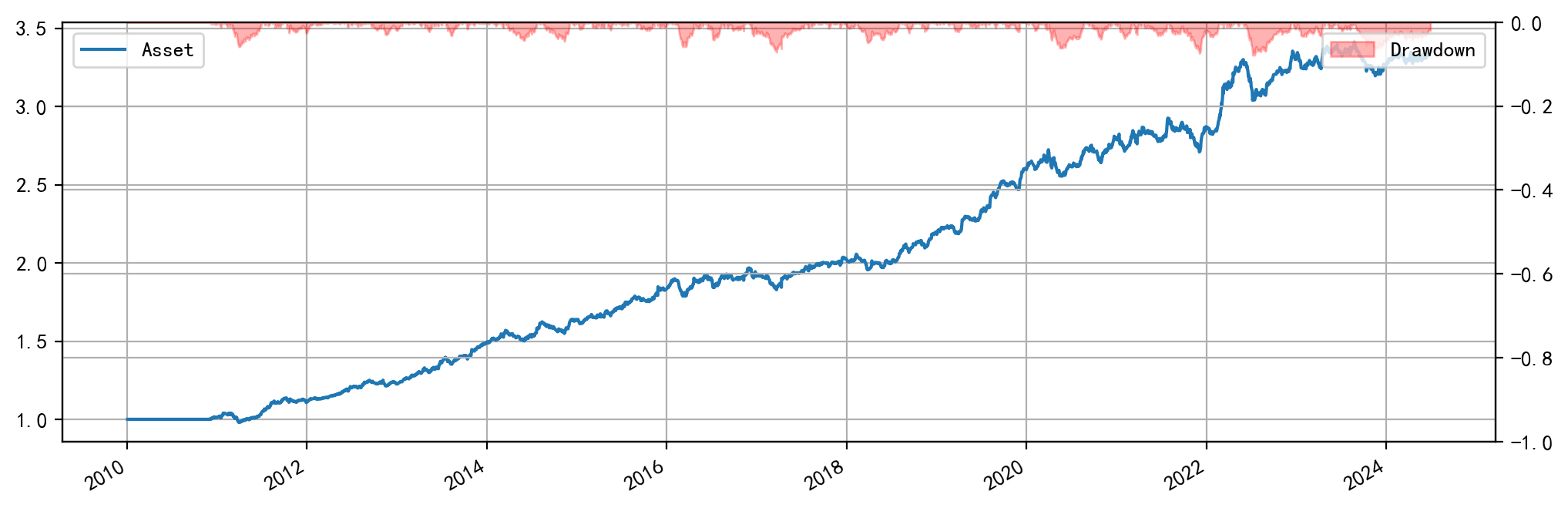
其他合约组合
对于最近月合约与次近月合约和次近月合约的组合,则在本地回测效果欠佳。比如,对于最近月合约与次近月合约组合,其因子效果对于参数更加敏感,且基本都带来负收益:
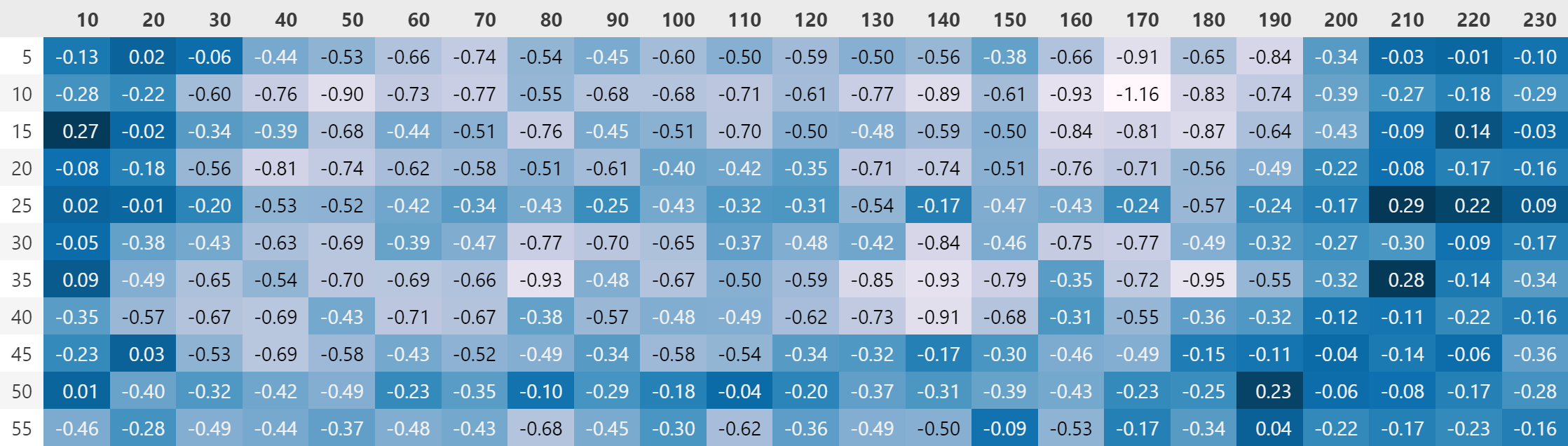
尝试 (25, 210) 这一本地回测结果为正的参数组合,本地回测结果如下:
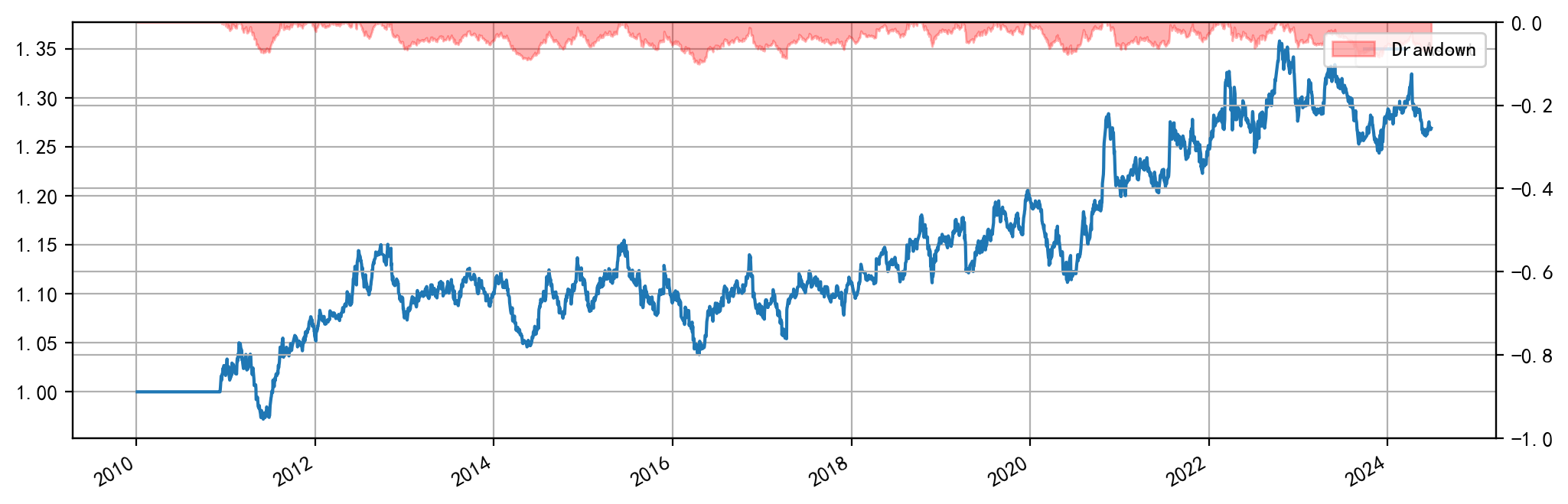
绩效尚可。但是由于参数的敏感性,这一收益曲线存在过拟合嫌疑。而尝试其他参数组合时,基本回测结果都很差劲。
总结
根据以上结果,无论使用展期收益率因子还是基差动量因子,都只有采用最近月合约与主力合约组合才能获得最稳健的收益。此外,我还稍微测试了一下因子在不同板块中的表现,似乎黑色板块相对是拖后腿的家伙,去掉这一板块之后,因子绩效倾向于变得更好。